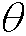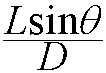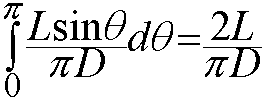Google收录页面数终于突破个位数了。百度收录了很多页面,但都是在blog.163.com域名下的。还是Google好,直接收录boleyn.su.blog.163.com的。
NOIP2010
最后一次NOIP了,390(最后一个程序dfs改快一点就可以400最后一个题有更好的算法,O(n^2)的)。
代码贴在这里,题解网上已经有了,就不必写了。
CODE:
/*
AUTHOR: Su Jiao
DATE: 2010-11-20
DESCRIPTION:
$DESCRIPTION
*/
#include <stdio.h>
#define PROBLEM “translate”
FILE* file;
const int QUEUE_SIZE=1<<20;
int M,N;
int queue[QUEUE_SIZE];
bool in_queue[QUEUE_SIZE];
int head,tail;
int answer;
int main()
{
file=fopen(PROBLEM“.in”,“r”);
fscanf(file,“%d%d”,&M,&N);
for (int i=0;i<N;i++)
{
int word;
fscanf(file,“%d”,&word);
if (!in_queue[word])
{
in_queue[queue[tail++]=word]=true;
if (tail-head>M)
in_queue[queue[head++]]=false;
answer++;
}
}
fclose(file);
file=fopen(PROBLEM“.out”,“w”);
fprintf(file,“%d\n”,answer);
fclose(file);
return 0;
}
#include <stdio.h>
#define PROBLEM “tortoise”
FILE* file;
const int MAXN=1<<10;
const int MAXCARD=1<<6;
const int MAXCARD_NUMBER=1<<3;
int N,M;
int a[MAXN];
int card[MAXCARD_NUMBER];
int f[MAXCARD][MAXCARD][MAXCARD][MAXCARD];
int main()
{
file=fopen(PROBLEM“.in”,“r”);
fscanf(file,“%d%d”,&N,&M);
for (int i=0;i<N;i++)
fscanf(file,“%d”,a+i);
for (int i=0;i<M;i++)
{
int b;
fscanf(file,“%d”,&b);
card[b]++;
}
fclose(file);
for (int i1=0;i1<=card[1];i1++)
for (int i2=0;i2<=card[2];i2++)
for (int i3=0;i3<=card[3];i3++)
for (int i4=0;i4<=card[4];i4++)
{
int get=a[1*i1+2*i2+3*i3+4*i4];
if (i1>0&&f[i1][i2][i3][i4]<f[i1-1][i2][i3][i4])
f[i1][i2][i3][i4]=f[i1-1][i2][i3][i4];
if (i2>0&&f[i1][i2][i3][i4]<f[i1][i2-1][i3][i4])
f[i1][i2][i3][i4]=f[i1][i2-1][i3][i4];
if (i3>0&&f[i1][i2][i3][i4]<f[i1][i2][i3-1][i4])
f[i1][i2][i3][i4]=f[i1][i2][i3-1][i4];
if (i4>0&&f[i1][i2][i3][i4]<f[i1][i2][i3][i4-1])
f[i1][i2][i3][i4]=f[i1][i2][i3][i4-1];
f[i1][i2][i3][i4]+=get;
}
file=fopen(PROBLEM“.out”,“w”);
fprintf(file,“%d\n”,f[card[1]][card[2]][card[3]][card[4]]);
fclose(file);
return 0;
}
#include <stdio.h>
#define PROBLEM “prison”
FILE* file;
const int MAXN=1<<20;
const int MAXM=1<<20;
const int UNCOLORED=-1,RED=0,BLUE=1;
struct Prison{int a,b,c;};
struct struct_edge{int v;struct_edge* n;};
typedef struct_edge* Edge;
int N,M;
Prison prison[MAXM];
Edge adj[MAXN];
struct_edge pool[MAXM*2];
Edge top;
int color[MAXN];
int answer=(~0u)>>1;
void quick_sort(int l,int r)
{
int i=l,j=r,mid=prison[(l+r)>>1].c;
while (i<=j)
{
while (i<=j&&prison[i].c>mid) i++;
while (i<=j&&prison[j].c<mid) j–;
if (i<=j)
{
Prison swap;
swap=prison[i],prison[i]=prison[j],prison[j]=swap;
i++,j–;
}
}
if (l<j) quick_sort(l,j);
if (i<r) quick_sort(i,r);
}
void add_edge(int u,int v)
{
top->v=v,top->n=adj[u],adj[u]=top++;
top->v=u,top->n=adj[v],adj[v]=top++;
}
void build_graph(int end)
{
top=pool;
for (int i=1;i<=N;i++) adj[i]=0;
for (int i=0;i<=end;i++)
add_edge(prison[i].a,prison[i].b);
}
bool color_node(int u,int which_color=RED)
{
if (color[u]!=UNCOLORED) return color[u]==which_color;
else
{
color[u]=which_color;
for (Edge i=adj[u];i;i=i->n)
if (!color_node(i->v,!which_color)) return false;
return true;
}
}
bool is_binary_graph()
{
for (int i=1;i<=N;i++) color[i]=UNCOLORED;
for (int i=1;i<=N;i++)
if (color[i]==UNCOLORED)
if (!color_node(i)) return false;
return true;
}
int main()
{
file=fopen(PROBLEM“.in”,“r”);
fscanf(file,“%d%d”,&N,&M);
for (int i=0;i<M;i++)
fscanf(file,“%d%d%d”,&prison[i].a,&prison[i].b,&prison[i].c);
fclose(file);
quick_sort(0,M-1);
int L=0,R=M;
while (L+1!=R)
{
int mid=(L+R)>>1;
build_graph(mid);
if (is_binary_graph()) L=mid;
else R=mid;
}
if (R!=M) answer=prison[R].c;
else answer=0;
file=fopen(PROBLEM“.out”,“w”);
fprintf(file,“%d\n”,answer);
fclose(file);
return 0;
}
#include <stdio.h>
#define PROBLEM “flow”
FILE* file;
const int MAXN=1<<10;
const int MAXM=1<<10;
const int oo=(~0u)>>1;
int N,M;
int height[MAXN][MAXM];
int color[MAXN][MAXM];
int adjs[MAXM];
int adj[MAXM][MAXM];
bool watered[MAXM];
int unwatered;
int begin[MAXM];
int end[MAXM];
int f[MAXM][MAXM];
int need;
void dfs(int x,int y,int start)
{
if (color[x][y]!=start)
{
color[x][y]=start;
if (height[x+1][y]<height[x][y]) dfs(x+1,y,start);
if (height[x-1][y]<height[x][y]) dfs(x-1,y,start);
if (height[x][y+1]<height[x][y]) dfs(x,y+1,start);
if (height[x][y-1]<height[x][y]) dfs(x,y-1,start);
if (x==N) adj[start][adjs[start]++]=y;
}
}
int main()
{
file=fopen(PROBLEM“.in”,“r”);
fscanf(file,“%d%d”,&N,&M);
for (int i=1;i<=N;i++)
for (int j=1;j<=M;j++)
fscanf(file,“%d”,height[i]+j);
fclose(file);
file=fopen(PROBLEM“.out”,“w”);
for (int i=1;i<=N;i++) height[i][0]=height[i][M+1]=oo;
for (int i=1;i<=M;i++) height[0][i]=height[N+1][i]=oo;
for (int i=1;i<=M;i++)
dfs(1,i,i);
for (int i=1;i<=M;i++)
for (int j=0;j<adjs[i];j++) watered[adj[i][j]]=true;
for (int i=1;i<=M;i++)
if (!watered[i]) unwatered++;
if (unwatered)
fprintf(file,“%d\n%d\n”,0,unwatered);
else
{
for (int i=1;i<=M;i++)
{
begin[i]=oo,end[i]=0;
for (int j=0;j<adjs[i];j++)
begin[i]=begin[i]<adj[i][j]?begin[i]:adj[i][j],
end[i]=end[i]>adj[i][j]?end[i]:adj[i][j];
}
f[0][0]=true;
for (int i=1;i<=M;i++)
if (begin[i]<=end[i])
for (int k=1;k<=M;k++)
{
if (f[k-1][end[i]]) f[k][end[i]]=true;
for (int j=begin[i]-1;j<=end[i];j++)
if (f[k-1][j]) f[k][end[i]]=true;
}
for (int i=1;i<=M;i++)
if (f[i][M])
{
need=i;
break;
}
fprintf(file,“%d\n%d\n”,1,need);
}
fclose(file);
return 0;
}
长为L的棍丢到有足够多的间距为D(D>L)的平行线的平面上,问棍落到线上的概率
64匹马能否通过50场比赛比出任意两匹马之间的优劣(每场比赛至多8匹马参赛)
这是2009年清华大学自主招生数学试题(理综)。
思考时间,答案在下面(字体是白色的)。
这道题其实考的是归并排序。
首先将马分为8组,每组排一下序,就比了8场。
然后再将这8组合并为4组,两两合并。
比如A和B组合并:
选A组的前4名和4个B组的前4名,比一场,如果从A中的选出的第4名比B中选出的第4名排名高,那么在A中的选出的第4名前和他自己一定是这些马中靠前的,于是把他们排到新的队中,其余马回到原来的位置;否则,同理分析。所以这样比一场可以确定至少4匹马在新的小组中的的位置。
接下来在剩下的马中继续这样做,直到所有马在新的小组中的位置都确定了。
由于每次都可以至少确定4匹马的位置,而且最后还剩8匹马时只需要比一次就可以确定8匹马的位置,所以两个8匹马的有序的小组合并为一个16匹马的有序小组只需要(16-8)/4+1=3次比赛。
所以8个8匹马的有序的小组合并为4个16匹马的有序小组需要4*3=12次比赛。
所以4个16匹马的有序的小组合并为2个32匹马的有序小组需要2*7=14次比赛。
所以2个32匹马的有序的小组合并为1个64匹马的有序小组需要1*15=15次比赛。
所以一共只需比49场就可以了。
请写出所有三个数均为质数,且公差为8的等差数列,并证明你的结论
这是2009年清华大学自主招生数学试题(理科)。
思考时间,答案在下面(字体是白色的)。
答案是3 11 19。
首先它是一个解,下面我们证明没有其它解。
设最小的一个数为X,那么数列为X,X+8,X+16。
然后
X mod 3 = X mod 3
X + 8 mod 3 = X+ 2 mod 3
X + 16 mod 3 =X + 1 mod 3
所以无论X为何值,这个数列中都有一个数是3的倍数,又它们都是质数,所以只可能是有一个数是3,那么显然这个问题解决了。
NOIP2009[Hankson的趣味题/son]
NOIP2010即将到来,这道题用来练练手感。
这道题的思路就是分解质因数。
首先,不难得到gcd(x/a1,a0/a1)=1以及gcd(b1/x,b1/b0)=1。
假设对于一个质因数y,a0含有a0c个y,a1含有a1c个y,b0含有b0c个y,b1含有b1c个y。
那么不难得到,如果a0c<a1c,那么就无解;如果a0c=a1c,那么x至少含有a1c个y;如果a0c>a1c,那么x只可能含有a1c个y。
同理,如果b1c<b0c,那么就无解;如果b1c=b0c,那么x至多含有b1c个y;如果b1c>b0c,那么x只可能含有b1c个y。
由此,可以求出对于每一个质数,x可能含有几个它,并求出一共有多少种选择方式。然后根据乘法原理,将每一个质数的选择方案数乘起来,就得到了答案。
CODE:
/*
AUTHOR: Su Jiao
DATE: 2010-10-14
DESCRIPTION:
$DESCRIPTION
*/
#include <stdio.h>
const int MAXSIZE=5000;
int prime_table[MAXSIZE];
int prime_table_size;
void initialize_prime_table()
{
prime_table_size=0;
prime_table[prime_table_size++]=2;
for (int i=3;prime_table_size<MAXSIZE;i++)
{
bool is_prime=true;
for (int j=0;j<prime_table_size;j++)
if (i%prime_table[j]==0)
{
is_prime=false;
break;
}
if (is_prime) prime_table[prime_table_size++]=i;
}
}
void calculate_one_step(int& a0,int& a1,int& b0,int& b1,int& result,int p)
{
int a0c=0,a1c=0,b0c=0,b1c=0;
while (a0%p==0) a0/=p,a0c++;
while (a1%p==0) a1/=p,a1c++;
while (b0%p==0) b0/=p,b0c++;
while (b1%p==0) b1/=p,b1c++;
if (a0c<a1c||b0c>b1c) result*=0;
else if (a0c==a1c&&b0c==b1c)
{
if (a1c<=b1c) result*=b1c-a1c+1;
else result*=0;
}
else if (a0c==a1c&&b0c<b1c)
{
if (a1c<=b1c) result*=1;
else result*=0;
}
else if (a0c>a1c&&b0c==b1c)
{
if (a1c<=b1c) result*=1;
else result*=0;
}
else //if (a0c>a1c&&b0c<b1c)
{
if (a1c==b1c) result*=1;
else result*=0;
}
}
int calculate(int a0,int a1,int b0,int b1)
{
//gcd(x/a1,a0/a1)=1
//gcd(b1/x,b1/b0)=1
if (a0%a1!=0||b1%b0!=0) return 0;
int result=1;
for (int i=0;i<prime_table_size;i++)
calculate_one_step(a0,a1,b0,b1,result,prime_table[i]);
if (a0!=1) calculate_one_step(a0,a1,b0,b1,result,a0);
else if (b1!=1&&b1!=a0) calculate_one_step(a0,a1,b0,b1,result,b1);
return result;
}
int main()
{
freopen(“son.in”,“r”,stdin);
freopen(“son.out”,“w”,stdout);
int n,a0,a1,b0,b1;
initialize_prime_table();
scanf(“%d”,&n);
for (int i=0;i<n;i++)
{
scanf(“%d%d%d%d”,&a0,&a1,&b0,&b1);
printf(“%d\n”,calculate(a0,a1,b0,b1));
}
return 0;
}
SGU107[987654321 problem]
先离线处理出在[0,10^9)内中所有平方末尾数为987654321的数,然后显然应该写成下面那样。
CODE:
/*
AUTHOR: Su Jiao
DATE: 2010-9-11
DESCRIPTION:
$DESCRIPTION
*/
#include <stdio.h>
int main()
{
/*
for (long long int i=0;i<1000000000;i++)
if (i*i%1000000000==987654321) printf(“%d\n”,int(i));
output:
111111111
119357639
380642361
388888889
611111111
619357639
880642361
888888889
*/
int n;
scanf(“%d”,&n);
if (n<=8) printf(“%d\n”,0);
else if (n==9) printf(“%d\n”,8);
else
{
printf(“%d”,72);
for (int i=10;i<n;i++) printf(“%d”,0);
printf(“\n”);
}
}
SGU106[The equation]
数学题。扩展欧几里得解模同余方程。
CO
/*
AUTHOR: Su Jiao
DATE: 2010-8-26
DESCRIPTION:
$DESCRIPTION
*/
#include <iostream>
#include <math.h>
using namespace std;
#define lli long long int
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define ceil_div(a,b) ceil(double(a)/double(b))
#define floor_div(a,b) floor(double(a)/double(b))
lli gcd(lli a,lli b,lli& x,lli& y)
{
//ax+by=gcd(a,b)
if (b==0)
{
x=1,y=0;
return a;
}
else
{
lli g=gcd(b,a%b,y,x);
//b*y+a%b*x=gcd(b,a%b)=gcd(a,b)
// b*y+a%b*x
//=b*y+(a-a/b*b)*x
//=b*y-a/b*b*x+a*x
//=a*x+b*(y-a/b*x)
y-=a/b*x;
return g;
}
}
lli get_answer(lli a,lli b,lli c,lli x1,lli x2,lli y1,lli y2)
{
//ax+by+c=0
if (!(x1<=x2&&y1<=y2)) return 0;
else if (a==0&&b==0)
return (c==0)*(x2-x1+1)*(y2-y1+1);
else if (a==0)
{
lli y=-c/b;
return ((b*y+c==0)&&(y1<=y&&y<=y2))*(x2-x1+1);
}
else if (b==0)
{
lli x=-c/a;
return ((a*x+c==0)&&(x1<=x&&x<=x2))*(y2-y1+1);
}
else
{
//a*x = c (mod b)
lli x,y,g;
g=gcd(a,b,x,y);//ax+by=g
if (c%g==0)
{
a/=g,b/=g,c/=g;//ax+by=1
x*=-c,y*=-c;//ax*(-c)+by*(-c)=-c
//set of root = {(x+b*k,y-a*k)}
lli rxa,rxb;
if (b>0) rxa=ceil_div(x1-x,b),rxb=floor_div(x2-x,b);
else rxa=ceil_div(x2-x,b),rxb=floor_div(x1-x,b);
lli rya,ryb;
if (a<0) rya=ceil_div(y-y1,a),ryb=floor_div(y-y2,a);
else rya=ceil_div(y-y2,a),ryb=floor_div(y-y1,a);
lli ra,rb;
ra=max(rxa,rya);
rb=min(rxb,ryb);
if (ra<=rb) return (rb-ra+1);
else return 0;
}
else return 0;
}
}
int main()
{
lli a,b,c,x1,x2,y1,y2;
cin>>a>>b>>c>>x1>>x2>>y1>>y2;
cout<<get_answer(a,b,c,x1,x2,y1,y2)<<endl;
}
SGU105[Div 3]
数学题。一个数能被3整除,当且仅当它的各位数的和能被3整除。
CODE:
/*
AUTHOR: Su Jiao
DATE: 2010-8-26
DESCRIPTION:
$DESCRIPTION
*/
#include <stdio.h>
int main()
{
int N;
scanf(“%d”,&N);
printf(“%d\n”,N/3*2+(N%3==2));
}
SGU104[Little shop of flowers]
动态规划经典题目,据说是IOI上出现的首个动态规划题目。
CODE:
/*
AUTHOR: Su Jiao
DATE: 2010-8-24
DESCRIPTION:
$DESCRIPTION
*/
#include <iostream>
using namespace std;
const int MAXF=100+2,MAXV=100+2;
const int oo=19930309;
int F,V;
int A[MAXF][MAXV];
int f[MAXF][MAXV];
void print(int v,int i)
{
if (i)
{
int j;
for (j=1;j<=V;j++)
if (f[i][j]==v)
break;
print(v-A[i][j],i-1);
cout<<j<<char(i==F?’\n’:’ ‘);
}
}
int main()
{
cin>>F>>V;
for (int i=1;i<=F;i++)
for (int j=1;j<=V;j++)
cin>>A[i][j];
#define max(a,b) ((a)>(b)?(a):(b))
for (int i=1;i<=F;i++)
for (int j=0;j<=V;j++)
{
f[i][j]=-oo;
for (int k=0;k<j;k++)
f[i][j]=max(f[i][j],f[i-1][k]+A[i][j]);
}
int answer=-oo;
for (int i=0;i<=V;i++)
answer=max(answer,f[F][i]);
cout<<answer<<endl;
print(answer,F);
}